[ACM_HDU_2046]骨牌铺方格

杰拉斯 | 时间：2012-03-31, Sat | 9,732 views
编程算法　

骨牌铺方格

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 14699 Accepted Submission(s): 7085

Description

在2×n的一个长方形方格中,用一个1× 2的骨牌铺满方格,输入n ,输出铺放方案的总数.
例如n=3时,为2× 3方格，骨牌的铺放方案有三种,如下图：

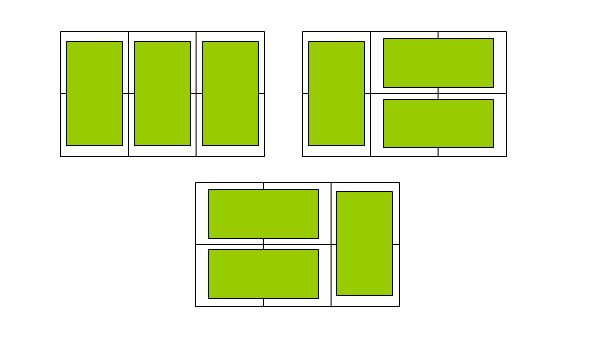
Input

输入数据由多行组成，每行包含一个整数n,表示该测试实例的长方形方格的规格是2×n (0<n<=50)。

Output

对于每个测试实例，请输出铺放方案的总数，每个实例的输出占一行。

Sample Input

1
3
2

Sample Output

1
3
2

Source

HDU2046

思路如下：

每新增一列，新增的放置方案有：

前n-1列的所有排列方案末端再加上一张竖牌；
前n-2列的所有排列方案末端再加上两张横牌。

即递推公式为：

f(n) = f(n - 1) + f(n - 2)

问题转换为求斐波那契数列。

#include<stdio.h>
int main(){
	int n;
	__int64 f[50];
	f[0] = 1;
	f[1] = 2;
	for(int i = 2; i < 50; ++i){
		f[i] = f[i - 1] + f[i - 2];
	}
	while(scanf("%d", &n) != EOF){
		printf("%I64d\n", f[n - 1]);
	}
	return 0;
}

应该注意的是后面的方案数量较大，不能使用int类型而应使用__int64类型，否则会因溢出而导致WA，还有使用printf输出时应是"%I64d"。

如需转载请注明出处：杰拉斯的博客

杰拉斯的博客